Dominio e Contradomínio de uma FUNÇÃO

O domínio de uma função é sempre o próprio conjunto de partida, ou seja, D = A. Se um objecto x pertence a A estiver associado a um elemento y  que pertence a B, dizemos que y é a imagem de x (indica-se y = f (x) e lê-se “y é igual a f de x”).



Exemplo:
se f é uma função de IN em IN (isto significa que o domínio e o contradomínio são os números naturais) definida por y = x+2. Então temos que:

• A imagem de 1 através de f é 3, ou seja, f(1)=1+2=3;

• A imagem de 2 através de f é 4, ou seja, f(2)=2+2=4;



De modo geral, a imagem de x através de f é x+2, ou seja: f(x) = x+2.

Numa função f de A em B, os elementos de B que são imagens dos elementos de A através da aplicação de f  formam o contradomínio de f.

Observações:
• Como x e y têm seus valores variando nos conjuntos A e B, recebem o nome de variáveis.

• A variável x é chamada variável independente e a variável y, variável dependente, pois para obter o valor de y dependemos de um valor de x.

• Uma função f  fica definida quando são dados seu domínio (conjunto A), seu contradomínio (conjunto B) e a função de transformação  y=f(x).

Noções de função

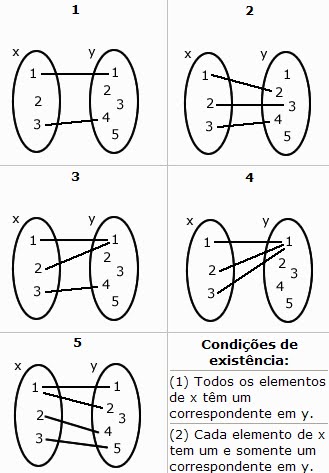
Considere os diagramas abaixo:

Vamos relembar que para existir uma  função, temos que verificar as seguintes condições:


(1) Todos os elementos de x têm um correspondente em y.
(2) Cada elemento de x tem um e somente um correspondente em y.

Analisando os diagramas acima:


O diagrama 1 não satisfaz a condição (1); os diagramas 3, 4 e 5 não satisfazem a condição (2).

Logo, concluímos que, somente o diagrama 2 representa uma função.

Funções

Função ou aplicação é um processo de transformação dos elementos de um conjunto A noutro conjunto B.

Ao falar em FUNÇÃO estamos então a considerar 3 situações:

 




Dá-se o nome de função a uma correspondência entre um conjunto A e um conjunto B que a cada elemento x do conjunto A faz corresponder um e um só elemento y do conjunto B.



Qualquer que seja a função, chama-se:
- Conjunto de partida ao conjunto A.
- Domínio de uma função ao conjunto de todos os valores da variável independente (ao conjunto A).
                Objectos aos elementos do domínio.



- Conjunto de chegada ao conjunto C.
- Contradomínio da função (conjunto B) ao conjunto de todos os valores da variável dependente (a todos os elementos do conjunto B que têm correspondência do conjunto A).
                         Imagens aos elementos do contradomínio.







Uma função pode representar-se por :
- uma tabela;
- um gráfico;
- uma expressão algébrica.

A semelhança de triângulos aplicada à vida real

A semelhança de triângulos tem inúmeras aplicações práticas, por exemplo:




Um topógrafo, para calcular a largura de um rio, sem atravessá-lo, faz uso do teodolito - aparelho para medir ângulos, estabelecendo uma distância de sua posição à margem do rio.

Com essas informações, desenha-se um triângulo semelhante às medidas traçadas ao rio.

Um pouco de história com Tales de Mileto e a semelhança de triângulos

Tales de Mileto, matemático e filósofo grego do século VI a.C., certa vez, apresentou-se ao Rei Amasis, do Egito, oferecendo-se para calcular a altura da pirâmide de Quéops, sem escalar o monumento. Nas proximidades da pirâmide, fincou uma estaca de madeira no solo.


Concluiu que, no momento em que o comprimento da sombra da pirâmide fosse igual ao comprimento da estaca, a altura da pirâmide seria igual ao comprimento da sombra da pirâmide mais metade da medida da base.

Qual foi o  raciocínio de Tales nas pirâmides?

O RACIOCÍNIO MATEMÁTICO DE TALES NA PIRÂMIDE foi o seguinte:

A pirâmide de Quéops, situada a dez milhas a Oeste do Cairo,  na planície de Gizéa 39 metros do vale do rio Nilo, foi construída a cerca de 2500 a.C.  Considerada uma das sete maravilhas domundo antigo, ela tem 146 m de altura. Sua base é um quadrado, cujos lados medem cerca de 230m.

Qual o CONCEITO MATEMÁTICO subjacente a este raciocínio?
“Se dois triângulos têm os ângulos respectivamente congruentes*, então seus lados são respectivamente proporcionais”

*Dizemos que dois ângulos são congruentes se, superpostos um sobre o outro, todos os seus elementos

coincidem.

Propriedade dos triângulos e regras de escrita (revisões)

Recorda:                                                                      

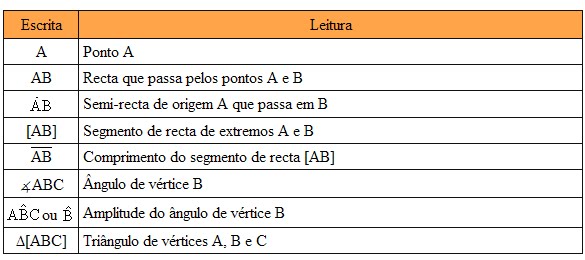
1º As regras de escrita:

2º Propriedade dos triângulos:

 A soma das amplitudes dos ângulos interno de um triângulo é sempre  igual a 180º.

120º + 35º + 25º = 180º

 
 Exercícios de revisão sobre a classificação dos angulos e regras de escrita