Boas férias....

O ano lectivo terminou,  os estágios e a PAF foram superados com sucesso, para aqueles que tiveram a  determinação de ir até ao fim...
Desejo a todos boas férias e  muita coragem para ultrapassar  os obstáculos que irão ter ao longo da vossa vida...Foi um prazer ser vossa professora.....

Diagrama ou gráfico Circular

Como o nome sugere esta representação é constituída por um círculo, em que se apresentam vários sectores circulares, tantos quanto as classes consideradas na tabela de frequências da amostra em estudo. Os ângulos dos sectores são proporcionais às frequências relativas das classes.

 Por exemplo, uma classe com uma frequência relativa igual a 0.20, terá no diagrama circular um sector com um ângulo igual a 360x0.20 = 72 graus. É uma representação utilizada essencialmente para dados qualitativos.



Exemplo: Categoria profissional dos funcionários de uma Escola Secundária

Classes  profissionais           Frequência absoluta       Frequência relativa      Amplitude dos ângulos
Auxiliar de Acção Educativa(AE)      20                                     0,47                     0,47 x 360º=169,2º
Administrativo (Ad)                          12                                      0,29                     0,29 x 360º=104,4º
Técnico de Acção Social (AS)           7                                       0,17                    0,17 x 360º=61,2º
Operário  (Op)                                   3                                      0,07                     0,07 x 360º=25,2º




 
Nesta representação, juntamente com a identificação da categoria, indica-se a frequência relativa da respectiva classe.

Medidas de tendência central: Média, Moda e Mediana

Chama-se Média de um conjunto de dados numéricos ao número que se obtém dividindo a soma dos valores de todos os dados pelo número de dados.




Consideremos a situação:

O Paulo, o António  e o Pedro são três avançados de uma equipa de futebol. Nesta época, o Paulo e o Pedro já fizeram cinco jogos e o António quatro.



O número de remates à baliza do adversário nos jogos realizados foi o seguinte:
Paulo: 7, 8, 3, 10, 7
António:  5, 5, 0, 4, 4
Pedro: 9, 8, 10, 5


Qual deles fez a melhor média?
Para calcular a média divide-se o nº total de remates pelo nº de jogos.

                                                                     
                                                          

                                           Paulo:                                  

                                           António:
                                                            
                                            Pedro:



Concluimos que o  Pedro fez a melhor média.






Chama-se Moda de um conjunto de dados ao dado que ocorre com maior frequência.
Para indicar a moda, observemos, de novo, os dados.


Para o Paulo a moda é 7, pois é o dado com maior frequência.
Para o António há duas modas: 4 e 5. Chama-se-lhe bimodal.
Para o Pedro não há moda; nenhum dos dados apresenta maior frequência que os outros. Neste caso dizemos que é amodal.



Observemos, de novo, os dados dos três avançados de uma equipa de futebol.

Para indicar a mediana começa-se por escrever os dados por ordem crescente ou decrescente.
A mediana é o valor central.


Para o Paulo: 7, 8, 3, 10, 7

António: 5, 5, 0, 4, 4

Pedro: 9, 8, 10, 5

Concluimos que:

--->  Se o número de dados é ímpar, a mediana é o valor que ocupa a posição central.
--->  Se o número de dados é par, a mediana é a média aritmética dos dois valores centrais.






Média, Moda e Mediana

Os gráficos de barras

Os gráficos são uma forma de apresentação visual dos dados. Normalmente, contém menos informações que as tabelas, mas são de mais fácil leitura.



 
 
Os Gráficos de barras são uma representação gráfica da distribuição de frequências absolutas ou relativas, onde os dados são representados por barras verticais ou horizontais com as seguintes características:  as barras têm a mesma largura e devem existir espaços entre as barras.


A altura ou o comprimento da barra é proporcional à frequência absoluta ou frequência relativa do acontecimento.



NB: Os gráficos de barras são usados para vários tipos de comparações.

Exemplo:

Tabela de frequências absolutas e relativas

A frequência absoluta, ou apenas frequência, de um valor é o número de vezes que uma determinada variável assume esse valor. Ao conjunto das frequências dos diferentes valores da variável dá-se o nome de distribuição da frequência (ou apenas distribuição).

A frequência relativa, é a percentagem relativa à frequência.
A frequência acumulada de um valor, é o numero de vezes que uma variável assume um valor inferior ou igual a esse valor.


A frequência relativa acumulada, é a percentagem relativa à frequência acumulada.



A tabela de frequências é uma forma de representação da frequência de cada valor distinto da variável. Juntamente com as frequências, esta poderá incluir frequências relativas, frequências acumuladas e frequências relativas acumuladas.




Exemplo: Consideremos a seguinte  informação

Nome..........  Sexo 
Paula.............. F
Gonçalo......... M
Manuel.......... M
Pedro............ M
Carla............. F
Cristina.......... F
Maria............ F
Sofia .............F
João............. M
Susana......... F



Resumindo, temos,

Sexo Masculino:
Frequência absoluta : 4
Frequência relativa: 4 em 10 = 40%

Sexo Feminino:
Frequência absoluta : 6
Frequência relativa: 6 em 10 = 60%

Assim a tabela de frequências da variável Sexo será:

ESTATÍSTICA

A Estatística é um ramo da Matemática que tem por objectivo obter, organizar e analisar dados, determinar as correlações que apresentem, tirando delas suas consequências para descrição e explicação do que passou e previsão e organização do futuro.

População: Conjunto de seres com uma característica comum, sobre o qual incide um estudo estatístico.
Amostra: Parte representativa da população sobre a qual incide a observação.


Exemplos:
1- Quando vais ao supermercado comprar cerejas, antes de comprares, provas uma – estás a utilizar uma amostra e a concluir que, a partir do sabor de uma (amostra), qual o sabor de todas as cerejas (população).
2- Quando visitas uma cidade, contactando com alguns dos seus habitantes, e de regresso, afirmas que as pessoas daquela cidade têm determinados atributos (simpáticas, hospitaleiras,...), estás a atribuir à população da cidade as características de uma amostra (as pessoas com quem contactaste).


Podemos concluir que quer num exemplo quer noutro, fez-se uma sondagem (utilizou-se uma amostra) e a partir das características da amostra, identificaram-se as características da população.


Frequência absoluta: Número de vezes que um dado acontecimento é observado.



Frequência relativa:Quociente entre a frequência absoluta de um dado acontecimento e o número total de elementos do estudo.



NOTA: Para obter a Frequência Relativa em Percentagem basta multiplicar por 100 a Frequência Relativa


Estatística

Dominio e Contradomínio de uma FUNÇÃO

O domínio de uma função é sempre o próprio conjunto de partida, ou seja, D = A. Se um objecto x pertence a A estiver associado a um elemento y  que pertence a B, dizemos que y é a imagem de x (indica-se y = f (x) e lê-se “y é igual a f de x”).



Exemplo:
se f é uma função de IN em IN (isto significa que o domínio e o contradomínio são os números naturais) definida por y = x+2. Então temos que:

• A imagem de 1 através de f é 3, ou seja, f(1)=1+2=3;

• A imagem de 2 através de f é 4, ou seja, f(2)=2+2=4;



De modo geral, a imagem de x através de f é x+2, ou seja: f(x) = x+2.

Numa função f de A em B, os elementos de B que são imagens dos elementos de A através da aplicação de f  formam o contradomínio de f.

Observações:
• Como x e y têm seus valores variando nos conjuntos A e B, recebem o nome de variáveis.

• A variável x é chamada variável independente e a variável y, variável dependente, pois para obter o valor de y dependemos de um valor de x.

• Uma função f  fica definida quando são dados seu domínio (conjunto A), seu contradomínio (conjunto B) e a função de transformação  y=f(x).

Noções de função

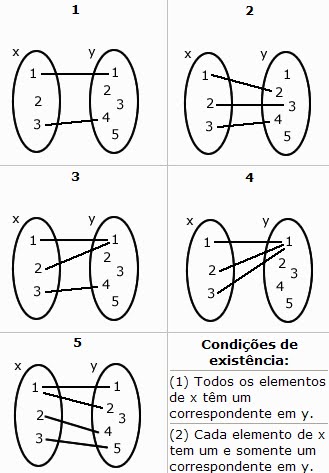
Considere os diagramas abaixo:

Vamos relembar que para existir uma  função, temos que verificar as seguintes condições:


(1) Todos os elementos de x têm um correspondente em y.
(2) Cada elemento de x tem um e somente um correspondente em y.

Analisando os diagramas acima:


O diagrama 1 não satisfaz a condição (1); os diagramas 3, 4 e 5 não satisfazem a condição (2).

Logo, concluímos que, somente o diagrama 2 representa uma função.

Funções

Função ou aplicação é um processo de transformação dos elementos de um conjunto A noutro conjunto B.

Ao falar em FUNÇÃO estamos então a considerar 3 situações:

 




Dá-se o nome de função a uma correspondência entre um conjunto A e um conjunto B que a cada elemento x do conjunto A faz corresponder um e um só elemento y do conjunto B.



Qualquer que seja a função, chama-se:
- Conjunto de partida ao conjunto A.
- Domínio de uma função ao conjunto de todos os valores da variável independente (ao conjunto A).
                Objectos aos elementos do domínio.



- Conjunto de chegada ao conjunto C.
- Contradomínio da função (conjunto B) ao conjunto de todos os valores da variável dependente (a todos os elementos do conjunto B que têm correspondência do conjunto A).
                         Imagens aos elementos do contradomínio.







Uma função pode representar-se por :
- uma tabela;
- um gráfico;
- uma expressão algébrica.

A semelhança de triângulos aplicada à vida real

A semelhança de triângulos tem inúmeras aplicações práticas, por exemplo:




Um topógrafo, para calcular a largura de um rio, sem atravessá-lo, faz uso do teodolito - aparelho para medir ângulos, estabelecendo uma distância de sua posição à margem do rio.

Com essas informações, desenha-se um triângulo semelhante às medidas traçadas ao rio.

Um pouco de história com Tales de Mileto e a semelhança de triângulos

Tales de Mileto, matemático e filósofo grego do século VI a.C., certa vez, apresentou-se ao Rei Amasis, do Egito, oferecendo-se para calcular a altura da pirâmide de Quéops, sem escalar o monumento. Nas proximidades da pirâmide, fincou uma estaca de madeira no solo.


Concluiu que, no momento em que o comprimento da sombra da pirâmide fosse igual ao comprimento da estaca, a altura da pirâmide seria igual ao comprimento da sombra da pirâmide mais metade da medida da base.

Qual foi o  raciocínio de Tales nas pirâmides?

O RACIOCÍNIO MATEMÁTICO DE TALES NA PIRÂMIDE foi o seguinte:

A pirâmide de Quéops, situada a dez milhas a Oeste do Cairo,  na planície de Gizéa 39 metros do vale do rio Nilo, foi construída a cerca de 2500 a.C.  Considerada uma das sete maravilhas domundo antigo, ela tem 146 m de altura. Sua base é um quadrado, cujos lados medem cerca de 230m.

Qual o CONCEITO MATEMÁTICO subjacente a este raciocínio?
“Se dois triângulos têm os ângulos respectivamente congruentes*, então seus lados são respectivamente proporcionais”

*Dizemos que dois ângulos são congruentes se, superpostos um sobre o outro, todos os seus elementos

coincidem.

Propriedade dos triângulos e regras de escrita (revisões)

Recorda:                                                                      

1º As regras de escrita:

2º Propriedade dos triângulos:

 A soma das amplitudes dos ângulos interno de um triângulo é sempre  igual a 180º.

120º + 35º + 25º = 180º

 
 Exercícios de revisão sobre a classificação dos angulos e regras de escrita

Aplicações da Semelhança de Triângulos

Por volta de 600 a .C. Tales de Mileto ( 640 a .C. - 550 a .C.) surpreendeu o faraó Amasis por se ter oferecido para determinar a altura da pirâmide de Quéops, sem ser necessário escalá-la.

Tales procedeu do seguinte modo: foi até a extremidade da sombra projectada pela grande pirâmide e cravou uma estaca no solo na vertical. A altura da pirâmide e a sua sombra seriam os lados de um triângulo rectângulo e o mesmo aconteceria com a estaca e a sua sombra.

Tales tinha consciência de que o método que acabara de utilizar era geral e podia ser empregue em muitas outras situações.

É possível determinar a altura “h” de uma montanha usando duas sombras de uma vareta de comprimento “v”.

Primeira sombra - h: v = d : s1

Segunda sombra - h: v = ( d + e + s2 ) : s2

E assim se obtém: d = s1( e + s2 ) /( s2 - s1 )

Triângulos semelhantes

Dois triângulos dizem-se semelhantes quando têm os ângulos respectivamente iguais e os lados homólogos proporcionais.


Porém, para se afirmar que dois triângulos são semelhantes, basta que se verifiquem apenas uma das condições ou  Critérios de Semelhança de Triângulos:




1º- Dois triângulos com os três lados proporcionais (ou os três ângulos iguais) são semelhantes.

2º- Dois triângulos com dois ângulos iguais são semelhantes.

Particularidades:
- Dois triângulos rectângulos que têm um ângulo agudo igual são semelhantes.
- Dois triângulos equiláteros são semelhantes.
- Dois triângulos isósceles que têm os ângulos opostos às bases iguais são semelhantes.
- Dois triângulos semelhantes a um terceiro são semelhantes entre si.





3° - Dois triângulos que têm dois lados proporcionais e o ângulo por eles formado igual são semelhantes.

Triângulos semelhantes

Ano Novo, novas atitudes ....

Iniciamos o segundo período, e tenho notado um empenho generalizado que espero perpetuar-se ao longo da vossa vida, peço-vos novamente para reverem no blogue toda a matéria relacionada com o Teorema de Pitágoras, têm vários links para consultar com exercícios....e não se esqueçam ...Ano Novo, novas atitudes...Bom estudo!!!

Boas Festas

Desejo-vos umas boas férias, aproveitem o vosso tempo para se divertir e descansar...

Provaram no final do período, que são um verdadeiro grupo e que a vossa capacidade é ilimitada quando traçam um objectivo e vencem um desafio...
Estou deveras muito orgulhosa do vosso trabalho e sei que no próximo ano 2010, que está quase a chegar, vai ser um ano de sucesso para todos vós, pois vão de certeza  dar continuidade ao vosso empenho...

Boas Festas!!!!!

exercícios resolvidos de aplicação do Teorema de Pitágoras

Nas postagens anteriores  observaste a demonstração do teorema de Pitágoras. Agora vais ver vários exemplos de aplicações do mesmo e em seguida, poderás resolver alguns exercícios propostos no link dos exercícios.





Exemplo 1:
Sendo a,b e c as medidas dos comprimentos dos lados de um triângulo, indica, justificando, aqueles que são rectângulos:
a) a = 6; b = 7 e c = 13;
b) a = 6; b = 10 e c = 8.



Resolução:
"Se num triângulo as medidas dos seus lados verificarem o Teorema de Pitágoras então pode-se concluir que o triângulo é rectângulo".Então teremos que verificar para cada alínea se as medidas dos lados dos triângulos satisfazem ou não o Teorema de Pitágoras.

a)

logo o triângulo não é rectângulo porque não satisfaz o Teorema de Pitágoras.

b)

logo o triângulo é rectângulo porque satisfaz o Teorema de Pitágoras.



Exemplo 2:
Calcula o valor de x em cada um dos triângulos rectângulos:


a)

b)

Resolução:
a) Aplicando o Teorema de Pitágoras temos:

b) Aplicando o Teorema de Pitágoras temos:

Exemplo 3:
Qual era a altura do poste?

Resolução:

Altura do poste é  4 (poste em pé) + 5 (poste partido)



Resposta: A altura do poste era de 9 m.





Exemplo 4:
O Pedro e o João estão a «andar» de baloiço, como indica a figura:

A altura máxima a que pode subir cada um dos amigos é de 60 cm.

Qual o comprimento do baloiço?



Resolução:

Pode-se aplicar o Teorema de Pitágoras, pois a linha a tracejado forma um ângulo de 90 graus com a "linha" do chão.



Então vem:
1,8 m = 180 cm

Resposta: O comprimento do baloiço é de aproximadamente 190 cm, isto é, 1,9 m.